What is Quicksort in Java?
The Quick Sort in Java is a sorting algorithm that belongs to the divide-and-conquer group.
It sorts in place (no need for extra data structures) and is not stable (it doesn’t guarantee the order of elements with the same value after sorting).
The divide-and-conquer algorithms make it easier to solve a problem by breaking it up into two or more smaller problems of the same type.
The breakdown keeps going until a problem is simple enough to be solved on its own (we call this the base case).
When working with large arrays, this algorithm has been shown to work best.
On the other hand, when working with smaller arrays, an algorithm like Selection Sort might work better.
Quicksort in Java Program
Quicksort In Java Program takes the basic idea of Selection Sort and changes it so that instead of a minimum (or a maximum), each element is put where it belongs in the sorted array at each step.
This part is known as the pivot. But if we wanted to use the divide-and-conquer method to reduce the problem of sorting the array into two smaller sub-arrays.
We’d have to do the following: while we’re putting our pivot in its place in the array, we’d have to divide the rest of the elements into two smaller groups: the ones to the left of the pivot are smaller or the same size as it, and the ones to the right are bigger than it.
This is the most important part of the algorithm. It’s called “partitioning,” and we have to do it well if we want Quicksort to work well too.
Before we talk about how Quicksort works, we need to talk about how the pivot is chosen.
The best case is when we always pick the element that divides the array into two equal parts.
But since this is almost impossible to do, there are a few different ways to solve this problem.
We can do this task in different ways, but the way we’ll do it in this article is to always pick the first (that is, the leftmost element of the array) as the pivot.
Now, let’s look at an example to show how everything works.
Visualizing Quicksort In Java
Imagine we have the following array:

In this case, the first iteration’s pivot will be 5, since the first element of the array is chosen as the pivot.
Now comes the parting: we need to put the number 5 where it will be found in the sorted array.
The position’s index will be 3, so after the first splitting, our array will look like this:

This is normal – whenever we split an array that isn’t the base case (size 1), the elements are clustered randomly.
The important part is what we stated earlier: the items left of the pivot are smaller or equal, while the elements on the right are bigger.
That doesn’t mean they can’t be sorted in the first grouping; it’s unlikely but possible.
We proceed and observe that divide-and-conquer kicks in – we can break down our original problem into two smaller ones.
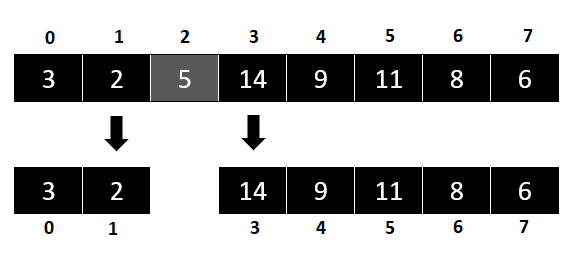
For the left problem, we have a two-element array, and the pivot element is 3.
After putting the pivot where it belongs (at position 2), we get the array [2, 3].
After that, there are no more cases on the left side of the problem, since the only subcases of [2, 3] are [2] and [3], which are both base cases.
This is the end of the left side of the subcases so that part of the array is now sorted.
On the right, the pivot point is 14. Since it’s the biggest number in the array we’re working with, we set it up like this:
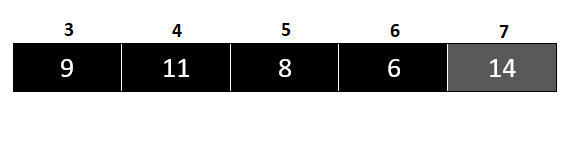
Not like before, when the pivot split our array into two subcases, [9, 11, 8, 6] is the only case here.
The pivot is currently at position 9, and we need to move it to position 6 in the array:
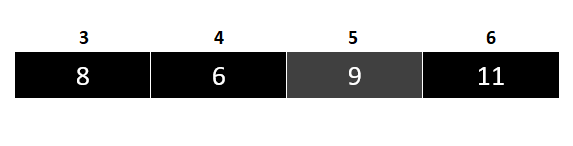
Now, the pivot divides the array into two parts: [7, 5] and [10]. Since [10] has only one element, this is our base case, and we don’t think about it at all.
The [7, 5] subarray is the only one left. Here, 7 is the pivot.
After moving it to its place (index 4), 5 is the only number to the left of it at index 3.
There are no more subcases, so the algorithm ends here.
After running Quicksort, the sorted list looks like this:
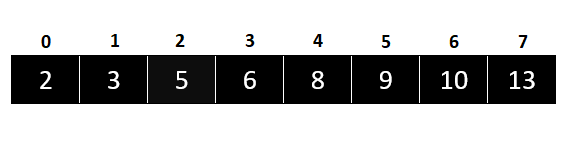
As you can see in the image, the sorting is completely done.
From the left side of all the elements, the numbers go from lowest to highest (2, 3, 5, 6, 8, 9, 10, 13), which means that the Quicksort worked perfectly and sorted everything perfectly.
Quicksort in Java Sample Code using Scanner
A Scanner is a class in the Java Utilities package that is used to get the input of primitive types like int, double, etc., and strings.
It is the easiest way to read input into a Java program.
/*
* To change this license header, choose License Headers in Project Properties.
* To change this template file, choose Tools | Templates
* and open the template in the editor.
*/
import java.util.Scanner;
/**
*
* @author glenn
*/
public class Quicksort_in_Java {
public static int partition(int a[], int l, int h) {
int i = l + 1, j = h, c = l, temp;
for (; i <= j;) {
while (i <= h && a[i] < a[c]) {
i++;
}
while (a[j] > a[c] && j > l) {
j--;
}
if (i < j) {
temp = a[i];
a[i] = a[j];
a[j] = temp;
} else {
break;
}
}
temp = a[c];
a[c] = a[j];
a[j] = temp;
return j;
}
public static void Sort(int a[], int l, int h) {
if (l < h) {
int m = partition(a, l, h);
Sort(a, l, m - 1);
Sort(a, m + 1, h);
}
}
public static void printarray(int a[]) {
for (int i = 0; i < a.length; i++) {
System.out.print(a[i] + " ");
}
}
/**
* @param args the command line arguments
*/
public static void main(String[] args) {
int n, res, i;
Scanner s = new Scanner(System.in);
System.out.print("Enter number of elements in the array:");
n = s.nextInt();
int a[] = new int[n];
System.out.println("Enter " + n + " elements ");
for (i = 0; i < n; i++) {
a[i] = s.nextInt();
}
System.out.println("elements in array ");
printarray(a);
Sort(a, 0, n - 1);
System.out.println("\nelements after sorting");
printarray(a);
}
}
Quicksort Example Output Using Scanner
Enter number of elements in the array:Enter 8 elements
elements in array
5 9 2 11 14 6 3 8
elements after sorting
2 3 5 6 8 9 11 14 You can test the above example here! ➡Java Online Compiler
Sample Java Code Using Array
An Array is a container object that holds a fixed number of values of the same type.
The length of an array is set when the array is made. After it is made, its length is fixed.
public class Quick
{
/* function that consider last element as pivot,
place the pivot at its exact position, and place
smaller elements to left of pivot and greater
elements to right of pivot. */
int partition (int a[], int start, int end)
{
int pivot = a[end]; // pivot element
int i = (start - 1);
for (int j = start; j <= end - 1; j++)
{
// If current element is smaller than the pivot
if (a[j] < pivot)
{
i++; // increment index of smaller element
int t = a[i];
a[i] = a[j];
a[j] = t;
}
}
int t = a[i+1];
a[i+1] = a[end];
a[end] = t;
return (i + 1);
}
/* function to implement quick sort */
void quick(int a[], int start, int end) /* a[] = array to be sorted, start = Starting index, end = Ending index */
{
if (start < end)
{
int p = partition(a, start, end); //p is partitioning index
quick(a, start, p - 1);
quick(a, p + 1, end);
}
}
/* function to print an array */
void printArr(int a[], int n)
{
int i;
for (i = 0; i < n; i++)
System.out.print(a[i] + " ");
}
public static void main(String[] args) {
int a[] = { 5, 9, 2, 11, 14, 6, 3, 8 };
int n = a.length;
System.out.println("\nBefore sorting array elements are - ");
Quick q1 = new Quick();
q1.printArr(a, n);
q1.quick(a, 0, n - 1);
System.out.println("\nAfter sorting array elements are - ");
q1.printArr(a, n);
System.out.println();
}
}
Quicksort Example Output using Array
Before sorting array elements are -
5 9 2 11 14 6 3 8
After sorting array elements are -
2 3 5 6 8 9 11 14 You can test the above example here! ➡Java Online Compiler
Anyway, if you want to level up your programming knowledge, especially Java, try this new article I’ve made for you Best Java Projects With Source Code For Beginners Free Download.
Conclusion
In this article, we’ve talked about how the Quicksort algorithm works, how it’s used, and how hard it is.
Even though the choice of the pivot can “make or break” this algorithm, it is usually thought of as one of the best sorting algorithms and is widely used when we need to sort arrays with a lot of elements.
Related Sorting Algorithm in Java
Inquiries
If you have any questions or suggestions about the Quicksort, please feel free to leave a comment below.


